What is Secure Multi-Party Computation?

This post is part of our Privacy-Preserving Data Science, Explained series.

As we mentioned in one of the previous posts in this series, federated learning is not enough to develop privacy-preserving ML applications. In fact, to keep the model from merely copying what it receives, the data needs to be kept secret while still permitting training and inference. One way to achieve this objective, with both significant advantages and trade-offs, is secret sharing in secure multi-party computation. Today we'll explore secure multi-party computation (SMPC) and explore how it can help us achieve input privacy. Similar to the post on FL, we hope that all the information in this article will be digestible for a broad audience, but section by section, we will go more into the weeds to understand and use this technique. For more info about the series, check out the intro article or take a look at the other posts to learn more about the technologies that can enable privacy-preserving ML with OpenMined's libraries.

Introduction

Broadly speaking, SMPC techniques are ways for parties to compute a function jointly while keeping their inputs secret. In the case of ML, this function might be a model’s loss function during training, or it could be the model itself in inference.

SMPC tends to have a significant communication overhead but has the advantage that, unless a substantial proportion of the parties are malicious and coordinating, the input data will remain private even if sought after for unlimited time and resources. Secret sharing in SMPC can protect both models' parameters and training/inference data.

Use cases

Machine Learning as a Service is one of the most significant use-cases of SMPC as it would allow companies to offer their models to perform inference on private data sent by their clients, while ensuring the utmost privacy. For example, in the medical field, a cloud service provider could run a trained classification model on secretly shared patient data and send the secretly shared result (e.g., a prediction of a disease) back to the patient.

Other notable applications of the technology involve non-intrusive, privacy-preserving security, i.e. systems capable of detecting nefarious activity from an encrypted and private data source. A useful metaphor for these systems is to think of them as the sniffer dogs of digital data sources. They don't infringe upon anyone's privacy thanks to the protection provided by secret sharing, their accuracy can be empirically verified, and since their parameters are kept private, they shouldn't be easily reverse engineered. For more info on this use case, check-out Andrew Trask's great blog post that goes more in-depth on similar applications using Homomorphic encryption to protect the data, secret sharing in SMPC can be used in much the same way.

Advantages:

• Can perform inference on encrypted data, so the model owner never sees the client's private data and therefore cannot leak it or misuse it.
• Not vulnerable to computationally powerful adversaries (e.g. intelligence agencies).
• Less computationally expensive and complex than Fully Homomorphic Encryption.

Disadvantages:

• Significant communications overhead.
• Assumptions need to be made about the proportions of malicious coordinating parties in the computation.

Implementation

PySyft implements secret sharing and fixed precision encoding, we'll detail both below but in PySyft they are two very simple tensor methods.

import torch as th
import syft as sy 
hook = sy.TorchHook(th)

alice = sy.VirtualWorker(hook, id="alice")
bob = sy.VirtualWorker(hook, id="bob")
secure_worker = sy.VirtualWorker(hook, id="secure_worker")<-- used to speed up computation by generating reliably random numbers

x = th.tensor([0.1, 0.2, 0.3])

x = x.fix_prec() <-- fixed precision encoding, turning floats into ints

x = x.share(alice, bob, secure_worker) <-- secret sharing by splitting the number in shares managed by independent entities 

Additive Secret Sharing

One of the easiest to understand implementations of secret sharing in SMPC is additive secret sharing, as explained in the Udacity course on Private AI.

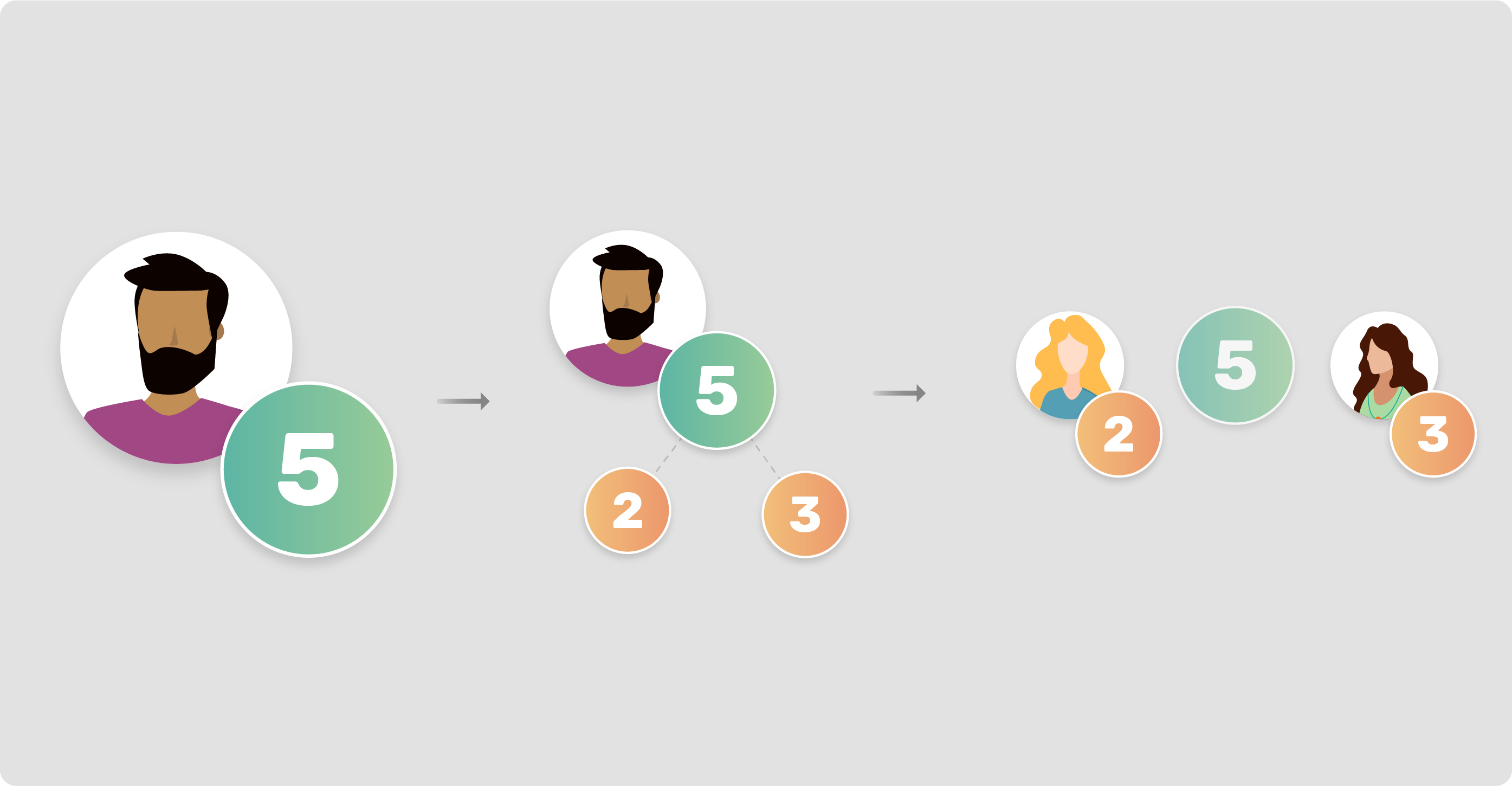
Additive secret sharing boils down to the idea that, a number let's say x=5, can be split in several shares let's say two,  share_1=2 and share_2=3, managed independently by two participants, let's call them Alice and Candice. At this point, if we were to apply any number of addition operations on the shares individually and then sum the results, this sum would be the same as applying those same additions and on x=5 .

To facilitate the encoding of negative numbers and increase the security of the protocol, we use the modulo operation with a very large prime number. The addition operations could also be performed with other encrypted numbers by adding up the shares of each of the addend. We can also perform multiplication between one encrypted number and a non encrypted number, by viewing the the operation as a series of additions.

import random

Q = 121639451781281043402593

def encrypt(x, n_shares = 2):
    shares = list()
    
    for i in range(n_shares-1):
        shares.append(random.randint(0,Q))
        
    final_share = Q - (sum(shares) % Q) + x
    
    share.append(final_share)
    
    return tuple(shares)
    
def decrypt(shares):
    return sum(shares) % Q
    
def add(a, b):
    c = list()
    
    assert(len(a) == len(b))
    
    for i in range(len(a)):
        c.append((a[i] + b[i]) % Q)
        
    return tuple(c)

SPDZ protocol

For multiplication between encrypted numbers PySyft implements the SPDZ protocol that is an extension of additive secret sharing, encrypt, decrypt and add are the same, but it enables more complex operations than addition.

Operations like multiplication where SPDZ manages to maintain the encrypted numbers private during the computation by using a triple of numbers generated by a crypto provider that is not otherwise involved in the computation. In the code at the beginning of the implementation section the crypto provider is secure_worker.

def generate_mul_triple():
    a = random.randrange(Q)
    b = random.randrange(Q)
    a_mul_b = (a * b) % Q
    return encrypt(a), encrypt(b), encrypt(a_mul_b)
    
#we also assume that the crypto provider distributes the shares

def mul(x, y):
    a, b, a_mul_b = generate_mul_triple()
    
    alpha = decrypt(x - a)<-x remains hidden because a is random 
    beta  = decrypt(y - b)<-y remains hidden because b is random 
    
    #local re-combination
    return alpha.mul(beta) + alpha.mul(b) + a.mul(beta) + a_mul_b

Taking a closer look at the operations we can see that since alpha * beta == xy - xb - ay + ab,  b * alpha == bx - ab, and a * beta == ay - ab if we add them all together and then sum a*b we will effectively return a privately shared version ofxy. For a more in-depth look at SPDZ and how it implements other functions check out these blog posts by Morten Dahl.

This schema appears quite simple, but it already permits all operations, as combinations of additions and multiplications, between two secretly shared numbers. Indeed, like the more complex Homomorphic encryption schemes that work with a single party,

SPDZ allows computation on ciphertexts generating an encrypted result which, when decrypted, matches the result of the operations as if they had been performed on the plaintext.

In this case, splitting the data into shares is the encryption, adding the shares back together is the decryption, while the shares are the ciphertext on which to operate.

This technique is adequate for integers, covering the encryption of things like the values of the pixels in images or the counts of entries in a database. The parameters of many ML models like neural networks, however, are floats, so how can we use additive secret sharing in ML?  We need to introduce a new ingredient, Fixed Precision Encoding, an intuitive technique that enables computation to be performed on floats encoded in integers values. In base 10 the encoding is as simple as removing the decimal point while keeping as many decimal places as indicated by the precision.

BASE=10
PRECISION=4

def encode(x):
    return int((x * (BASE ** PRECISION)) % Q)

def decode(x):
    return (x if x <= Q/2 else x - Q) / BASE**PRECISION
    
encode(3.5) <-- 35000
decode(35000) <-- 3.5

SMPC in PyGrid

SMPC is also one of the pillars of PyGrid, OpenMined's peer-to-peer platform that uses the PySyft framework for Federated Learning and data science. The platform uses secure multiparty computation in cases when the overhead in communication is manageable, for example, when using a model only for inference. In those cases, this technique protects both data and model's parameters and enables the kind of Private MLaaS applications that we introduced in this article.

OpenMined would like to thank Antonio Lopardo, Emma Bluemke, Théo Ryffel, Nahua Kang, Andrew Trask, Jonathan Lebensold, Ayoub Benaissa, and Madhura Joshi, Shaistha Fathima, Nate Solon, Robin Röhm, Sabrina Steinert, Michael Höh and Ben Szymkow for their contributions to various parts of this series.