This post is part of our Privacy-Preserving Data Science, Explained series.
CKKS explained series
Part 1, Vanilla Encoding and Decoding
Part 2, Full Encoding and Decoding
Part 3, Encryption and Decryption
Part 4, Multiplication and Relinearization
Part 5, Rescaling
Introduction
Homomorphic encryption is a promising field which allows computation on encrypted data. This excellent post, What Is homomorphic Encryption, provides a broad explanation of what homomorphic encryption is and what the stakes are for this field of research.
In this series of articles, we will study in depth the Cheon-Kim-Kim-Song (CKKS) scheme, which is first discussed in the paper Homomorphic Encryption for Arithmetic of Approximate Numbers. CKKS allows us to perform computations on vectors of complex values (thus real values as well). The idea is that we will implement CKKS from scratch in Python and then, by using these crypto primitives, we can explore how to perform complex operations such as linear regression, neural networks, and so on.

The figure above provides a high-level view of CKKS. We can see that a message m, a vector of values on which we want to perform certain computation, is first encoded into a plaintext polynomial p(X) and then encrypted using a public key.
CKKS works with polynomials because they provide a good trade-off between security and efficiency as compared to standard computations on vectors.
Once the message m is encrypted into c, a couple of polynomials, CKKS provides several operations that can be performed on it, such as addition, multiplication and rotation.
If we denote a function by f, which is a composition of homomorphic operations, then decrypting c’ = f(c) with the secret key will yield p’ = f(p). Therefore once we decode it, we will get m = f(m).
The central idea to implement a homomorphic encryption scheme is to have homomorphic properties on the encoder, decoder, encryptor and decryptor. This way, operations on ciphertext will be decrypted and decoded correctly and provide outputs as if operations were done directly on plaintext.
So in this article we will see how to implement the encoder and the decoder, and in later articles we will continue to implement the encryptor and decryptor to have a homomorphic encryption scheme.
Preliminaries
Basic knowledge in linear algebra and ring theory is recommended to have a good understanding of how CKKS is implemented. You can acquaint yourself with these topics using the following links:
- Introduction to linear algebra provides a good basis in linear algebra.
- Ring theory (Math 113) is a good resource to learn ring theory.
Specifically for this article, we will rely on the following concepts:
- Cyclotomic polynomials which are polynomials with nice properties, as they allow efficient computations when used as polynomial modulo.
- Canonical embedding which is used for encoding and decoding. They have the nice properties of being isomorphism, i.e. one-to-one homomorphisms between vectors and polynomials.
- Vandermonde matrices which are a special class of matrices, which we will use to have the inverse of the canonical embedding.
If you want to run the notebook you can find it in this Colab notebook.
Encoding in CKKS
CKKS exploits the rich structure of integer polynomial rings for its plaintext and ciphertext spaces. Nonetheless, data comes more often in the form of vectors than in polynomials.
Therefore, it is necessary to encode our input \(z \in \mathbb{C}^{N/2}\) into a polynomial \(m(X) \in \mathbb{Z}[X]/(X^N + 1)\).
We will denote the degree of our polynomial degree modulus by \(N\), which will be a power of 2. We denote the \(m\)-th cyclotomic polynomial (note that \(M=2N\)) by \(\Phi_M(X) = X^N + 1\). The plaintext space will be the polynomial ring \(\mathcal{R} = \mathbb{Z}[X]/(X^N + 1)\). Let us denote by \(\xi_M\), the \(M\)-th root of unity : \(\xi_M = e^{2 i \pi / M}\).
To understand how we can encode a vector into a polynomial and how the computation performed on the polynomial will be reflected in the underlying vector, we will first experiment with a vanilla example, where we simply encode a vector \(z \in \mathbb{C}^{N}\) into a polynomial \(m(X) \in \mathbb{C}[X]/(X^N + 1)\). Then we will cover the actual encoding of CKKS, which takes a vector \(z \in \mathbb{C}^{N/2}\), and encodes it in a polynomial \(m(X) \in \mathbb{Z}[X]/(X^N + 1)\).
Vanilla Encoding
Here we will cover the simple case of encoding \(z \in \mathbb{C}^{N}\), into a polynomial \(m(X) \in \mathbb{C}[X]/(X^N + 1)\).
To do so, we will use the canonical embedding \(\sigma : \mathbb{C}[X]/(X^N +1) \rightarrow \mathbb{C}^N\), which decodes and encodes our vectors.
The idea is simple: To decode a polynomial \(m(X)\) into a vector \(z\), we evaluate the polynomial on certain values, which will be the roots of the cyclotomic polynomial \(\Phi_M(X) = X^N + 1\). Those \(N\) roots are : \(\xi, \xi^3, ..., \xi^{2 N - 1}\).
So to decode a polynomial \(m(X)\), we define \(\sigma(m) = (m(\xi), m(\xi^3), ..., m(\xi^{2 N - 1})) \in \mathbb{C}^N\). Note that \(\sigma\) defines an isomorphism, which means it is a bijective homomorphism, so any vector will be uniquely encoded into its corresponding polynomial, and vice-versa.
The tricky part is the encoding of a vector \(z \in \mathbb{C}^N\) into the corresponding polynomial, which means computing the inverse \(\sigma^{-1}\). Hence, the problem is to find a polynomial \(m(X) = \sum_{i=0}^{N-1} \alpha_i X^i \in \mathbb{C}[X]/(X^N + 1)\), given a vector \(z \in \mathbb{C}^N\), such that \(\sigma(m) = (m(\xi), m(\xi^3), ..., m(\xi^{2 N - 1})) = (z_1,...,z_N)\).
Pursuing this thread further, we end up with the following system :
\(\sum_{j=0}^{N-1} \alpha_j (\xi^{2 i - 1})^j = z_i, i=1,...,N\).
This can be viewed as a linear equation :
\(A \alpha = z\), with \(A\) the Vandermonde matrix of the \((\xi^{2 i -1})_{i=1,...,N}\), \(\alpha\) the vector of the polynomial coefficients, and \(z\) the vector we want to encode.
Therefore we have that : \(\alpha = A^{-1} z\), and that \(\sigma^{-1}(z) = \sum_{i=0}^{N-1} \alpha_i X^i \in \mathbb{C}[X]/(X^N + 1)\).
Example
Let's now examine an example to better understand what we have discussed so far.
Let \(M = 8\), \(N = \frac{M}{2}= 4\), \(\Phi_M(X) = X^4 + 1\), and \(\omega = e^{\frac{2 i \pi}{8}} = e^{\frac{i \pi}{4}}\).
Our goal here is to encode the following vectors : \([1, 2, 3, 4]\) and \([-1, -2, -3, -4]\), decode them, add and multiply their polynomial and decode it.
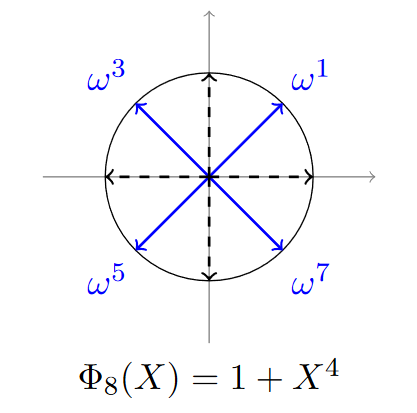
As we can see, in order to decode a polynomial, we simply need to evaluate it on powers of an \(M\)-th root of unity. Here we choose \(\xi_M = \omega = e^{\frac{i \pi}{4}}\).
Once we have \(\xi\) and \(M\), we can define both \(\sigma\) and its inverse \(\sigma^{-1}\), respectively the decoding and the encoding.
Implementation
Now we can move on to implement the Vanilla Encoder and Decoder in Python.
import numpy as np
# First we set the parameters
M = 8
N = M //2
# We set xi, which will be used in our computations
xi = np.exp(2 * np.pi * 1j / M)
xi(0.7071067811865476+0.7071067811865475j)
from numpy.polynomial import Polynomial
class CKKSEncoder:
"""Basic CKKS encoder to encode complex vectors into polynomials."""
def __init__(self, M: int):
"""Initialization of the encoder for M a power of 2.
xi, which is an M-th root of unity will, be used as a basis for our computations.
"""
self.xi = np.exp(2 * np.pi * 1j / M)
self.M = M
@staticmethod
def vandermonde(xi: np.complex128, M: int) -> np.array:
"""Computes the Vandermonde matrix from a m-th root of unity."""
N = M //2
matrix = []
# We will generate each row of the matrix
for i in range(N):
# For each row we select a different root
root = xi ** (2 * i + 1)
row = []
# Then we store its powers
for j in range(N):
row.append(root ** j)
matrix.append(row)
return matrix
def sigma_inverse(self, b: np.array) -> Polynomial:
"""Encodes the vector b in a polynomial using an M-th root of unity."""
# First we create the Vandermonde matrix
A = CKKSEncoder.vandermonde(self.xi, M)
# Then we solve the system
coeffs = np.linalg.solve(A, b)
# Finally we output the polynomial
p = Polynomial(coeffs)
return p
def sigma(self, p: Polynomial) -> np.array:
"""Decodes a polynomial by applying it to the M-th roots of unity."""
outputs = []
N = self.M //2
# We simply apply the polynomial on the roots
for i in range(N):
root = self.xi ** (2 * i + 1)
output = p(root)
outputs.append(output)
return np.array(outputs)Let's first encode a vector and see how it is encoded using real values.
# First we initialize our encoder
encoder = CKKSEncoder(M)
b = np.array([1, 2, 3, 4])
barray([1, 2, 3, 4])
Let's encode the vector now.
p = encoder.sigma_inverse(b)
px↦(2.5+4.440892098500626e-16j)+((-4.996003610813204e-16+0.7071067811865479j))x+((-3.4694469519536176e-16+0.5000000000000003j))x^2+((-8.326672684688674e-16+0.7071067811865472j))x^3
Now let's see how we can extract the vector we had initially from the polynomial:
b_reconstructed = encoder.sigma(p)
b_reconstructedarray([1.-1.11022302e-16j, 2.-4.71844785e-16j, 3.+2.77555756e-17j, 4.+2.22044605e-16j])
We can see that the values of the reconstruction and the initial vector are very close.
np.linalg.norm(b_reconstructed - b)6.944442800358888e-16
As stated before, \(\sigma\) is not chosen randomly to encode and decode, but it has a lot of nice properties. Among them, \(\sigma\) is an isomorphism, so addition and multiplication on polynomials will result in coefficient wise addition and multiplication on the encoded vectors.
The homomorphic property of \(\sigma\) is due to the fact that \(X^N + 1 = 0\) and \(\xi^N + 1 = 0\).
We can now start to encode several vectors, and see how we can perform homomorphic operations on them and decode it.
m1 = np.array([1, 2, 3, 4])
m2 = np.array([1, -2, 3, -4])
p1 = encoder.sigma_inverse(m1)
p2 = encoder.sigma_inverse(m2)We can see that addition is pretty straightforward.
p_add = p1 + p2
p_addx↦(2.0000000000000004+1.1102230246251565e-16j)+((-0.7071067811865477+0.707106781186547j))x+((2.1094237467877966e-15-1.9999999999999996j))x^2+((0.7071067811865466+0.707106781186549j))x^3
Here as expected, we see that p1 + p2 decodes correctly to \([2, 0, 6, 0]\).
encoder.sigma(p_add)array([2.0000000e+00+3.25176795e-17j, 4.4408921e-16-4.44089210e-16j, 6.0000000e+00+1.11022302e-16j, 4.4408921e-16+3.33066907e-16j])
Because when doing multiplication we might have terms whose degree is higher than \(N\), we will need to do a modulo operation using \(X^N + 1\).
To perform multiplication, we first need to define the polynomial modulus which we will use.
poly_modulo = Polynomial([1,0,0,0,1])
poly_modulox↦1.0+0.0x+0.0x^2+0.0x^3+1.0x^4
Now we can perform multiplication.
p_mult = p1 * p2 % poly_moduloFinally if we decode it, we can see that we have the expected result.
encoder.sigma(p_mult)array([ 1.-8.67361738e-16j, -4.+6.86950496e-16j, 9.+6.86950496e-16j, -16.-9.08301212e-15j])
Therefore we can see that our simple encoder and decoder works as expected, as it has homomorphic properties and is a one-to-one mapping between vectors and polynomials.
While this is a great step, we have actually lied because if you noticed before, when we used the encoder \(\sigma^{-1}\) the polynomials had complex coefficients. So while the encoder and decoder were indeed homomorphic and one-to-one, the domains they covered were \(\mathbb{C}^N \rightarrow \mathbb{C}[X]/(X^N +1)\). Because we actually want polynomials to belong in \(\mathbb{Z}[X]/(X^N +1)\) to use all the properties of integer polynomial rings, we thus need to make sure the encoder outputs polynomials with integer coefficients and not complex coefficients.
So I hope you enjoyed this little introduction to encoding complex numbers into polynomials for homomorphic encryption. We will see in the next article how to implement the actual encoder and decoder used in CKKS so stay tuned !





