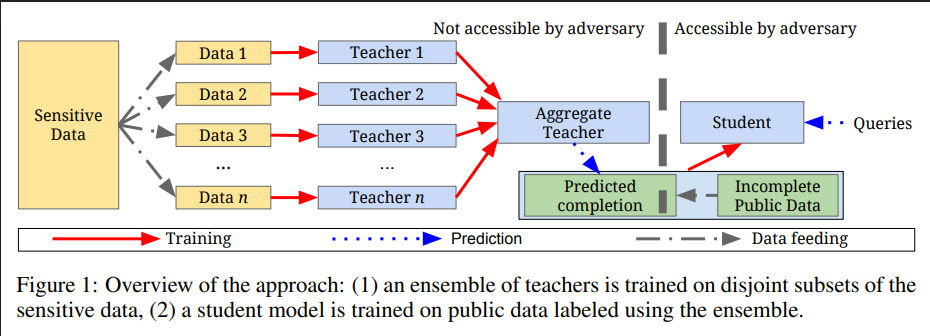
Summary: In this blog we’re going to discuss PATE - "Private Aggregation of Teacher Ensembles". PATE is a private machine learning technique created by Nicolas Papernot et. al., published in ICLR 2018. In financial or medical applications, performing machine learning involves sensitive data. PATE is an approach to perform machine learning on this kind of sensitive data with different notions of privacy guarantees involved. In PATE we need to split the sensitive data into a certain number. of training sets and train a classifier on each of those sets. Then we need to use the classifiers to predict the labels of the public data.
Let us discuss some challenges of performing machine Learning on Private data. Here are some attacks that have been seen in the security literature.
1) Training data extraction attacks or model inversion attacks: Imagine you have a classifier trained on images of individual faces, to recognize which individual is in the image, you feed the classifier some face images and the output will classify the person in the image. Frederikson. et. al. showed that with access to the classifier’s output probabilities they were able to reconstruct these images here which are approximations of the training data that the machine learning classifier saw. These approximations are not extracting individual training points but rather the average representations that the classifier learned for each class which here corresponds to one individual.
2) Membership attacks: The second kind of attack is membership inference attacks against ML models introduced by Shokri et. al.. Here the goal of the adversary is slightly different, instead of reconstructing training points from the output of the classifier the goal now is to infer whether a specific input was used to train the model. Given the image of a person, did the person contribute to the training data from a specific machine learning model. What Shokri et.al. also showed is that you can perform these attacks by only having access to the classifier’s probabilities.
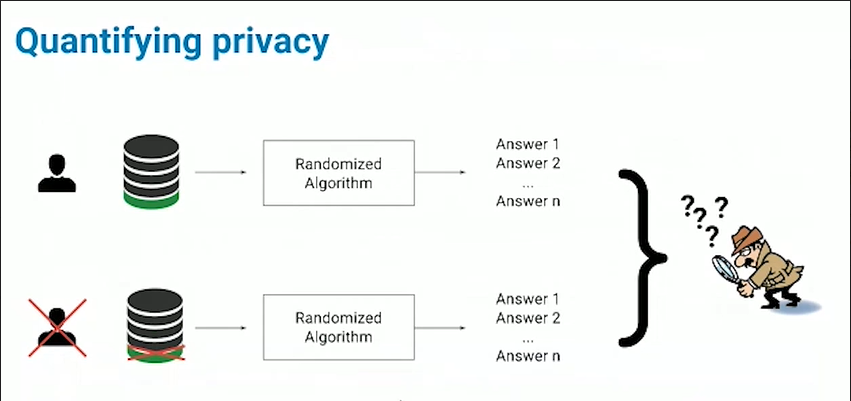
PATE analysis is a way to defend these data holders against these powerful attackers by generally considering two types of threat models i.e. black box and white box adversaries:
1) Model querying (black-box-adversary): In this kind of attack, the adversary is only able to query the model that you trained, it will not have access to the internals of the model or to the architectures to the parameters. All it can do is submit inputs to your black-box model and observe the prediction that the model is making. This is called model querying attacks or black box attacks. The two attacks presented above are instances of such attacks.(Shokri et.al. & Frederikson et.al.)
2) Model inspection (white-box adversary): This kind of attack is stronger because in this case the adversary has access to the model and its parameters. The work by Zhang et.al. i.e Understanding Deep Learning requires re-thinking generalization kind of hints at the fact that machine learning models might be able to memorize some of their training data or at least they have the capacity to do so. So we need to be robust to an attacker that has access to these model parameters and can analyze them.
This is why while working on PATE analysis the threat models considered are very powerful adversaries, which can make a potentially unbounded number of queries and also have access to the model internals.
The way it is proved that PATE provides differential privacy is based on an application called "Moments Accountant", a technique introduced by Abadi et. al. in 2016 paper. The Moments accountant technique allows us to formalize the fact that when we have a strong quorum among the teachers - when all of the teachers or most of the teachers agree - then we should pay a small privacy cost for that prediction given to the student. The guarantees we provide here in terms of differential privacy are "data dependant", which means that during training all the votes provided by the teachers are recorded and we compute numerical values for the differential privacy guarantees provided. Here, in a sense, differential privacy is characterized by two values epsilon and delta.
Epsilon, or the privacy budget, is the value which basically defines an interval, which quantifies how much we tolerate the output of the machine learning model on one database to be different from the output of the same machine learning model on second database D prime that only has one training point that is different. The smaller the epsilon is, the stronger the privacy will be.
Delta is the failure rate which we tolerate the guarantee to not hold.

Step by Step Tutorial
The first thing we need to do before getting started is install syft
!pip install syftLoad the SVHN data set
SVHN is a real-world image data set for developing machine learning and object recognition algorithms with minimal requirement on data preprocessing and formatting. It can be seen as similar in flavor to MNIST (e.g., the images are of small cropped digits), but incorporates an order of magnitude more labeled data (over 600,000 digit images) and comes from a significantly harder, unsolved, real world problem (recognizing digits and numbers in natural scene images). SVHN is obtained from house numbers in Google Street View images.italicized text.
import torch
from torchvision import datasets, transforms
from torch.utils.data import Subset
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
train_data = datasets.SVHN('datasets/SVHN/train/', split='train', transform=transform,
target_transform=None, download=True)
test_data = datasets.SVHN('datasets/SVHN/test/', split='test', transform=transform,
target_transform=None, download=True)
num_teachers = 100
batch_size = 50
def get_data_loaders(train_data, num_teachers):
""" Function to create data loaders for the Teacher classifier """
teacher_loaders = []
data_size = len(train_data) // num_teachers
for i in range(data_size):
indices = list(range(i*data_size, (i+1)*data_size))
subset_data = Subset(train_data, indices)
loader = torch.utils.data.DataLoader(subset_data, batch_size=batch_size)
teacher_loaders.append(loader)
return teacher_loaders
teacher_loaders = get_data_loaders(train_data, num_teachers)Generating the student train and test data by splitting the svhn test set
student_train_data = Subset(test_data, list(range(9000)))
student_test_data = Subset(test_data, list(range(9000, 10000)))
student_train_loader = torch.utils.data.DataLoader(student_train_data, batch_size=batch_size)
student_test_loader = torch.utils.data.DataLoader(student_test_data, batch_size=batch_size)Define the teacher models and train them by defining a cnn
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(5*10*10, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(x.size(0), 5*10*10)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x)Defining the train and predict functions
def train(model, trainloader, criterion, optimizer, epochs=10):
running_loss = 0
for e in range(epochs):
model.train()
for images, labels in trainloader:
optimizer.zero_grad()
output = model.forward(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
def predict(model, dataloader):
outputs = torch.zeros(0, dtype=torch.long)
model.eval()
for images, labels in dataloader:
output = model.forward(images)
ps = torch.argmax(torch.exp(output), dim=1)
outputs = torch.cat((outputs, ps))
return outputs
def train_models(num_teachers):
models = []
for i in range(num_teachers):
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
train(model, teacher_loaders[i], criterion, optimizer)
models.append(model)
return models
models = train_models(num_teachers)Next by combining the predictions of the Teacher models we will generate the Aggregated Teacher and Student labels
import numpy as np
epsilon = 0.2
def aggregated_teacher(models, dataloader, epsilon):
preds = torch.torch.zeros((len(models), 9000), dtype=torch.long)
for i, model in enumerate(models):
results = predict(model, dataloader)
preds[i] = results
labels = np.array([]).astype(int)
for image_preds in np.transpose(preds):
label_counts = np.bincount(image_preds, minlength=10)
beta = 1 / epsilon
for i in range(len(label_counts)):
label_counts[i] += np.random.laplace(0, beta, 1)
new_label = np.argmax(label_counts)
labels = np.append(labels, new_label)
return preds.numpy(), labels
teacher_models = models
preds, student_labels = aggregated_teacher(teacher_models, student_train_loader, epsilon)Now by using the labels generated previously we will create the Student model and train it
Why do we need to train an additional student model? The aggregated teacher violates our threat model:
- The total privacy loss gets increased by each prediction. Privacy budgets create a tension between the accuracy and number of predictions. (If we stick to the first part of the mechanism where we have only the teachers, everytime the teachers make a prediction we pay an additional cost in privacy. As users make more and more prediction queries the overall cost in terms of privacy will keep increasing so at some point we will have a tension between utility and privacy.)
- Private data may get revealed by the inspection of internals. Privacy guarantees should hold in the face of white-box adversaries. (If you remember a threat model we considered adversaries are able to access the internals of the models which means that if the adversaries are able to inspect the internals of the teachers because the teachers saw the training data they may be able to leak some information about that training data. Whereas if the adversary instead inspects the student model then it will only be able recover, in the worst case, the public data with the labels that were provided by the teachers with differential privacy.)
def student_loader(student_train_loader, labels):
for i, (data, _) in enumerate(iter(student_train_loader)):
yield data, torch.from_numpy(labels[i*len(data): (i+1)*len(data)])
student_model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(student_model.parameters(), lr=0.003)
epochs = 10
steps = 0
running_loss = 0
for e in range(epochs):
student_model.train()
train_loader = student_loader(student_train_loader, student_labels)
for images, labels in train_loader:
steps += 1
optimizer.zero_grad()
output = student_model.forward(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if steps % 50 == 0:
test_loss = 0
accuracy = 0
student_model.eval()
with torch.no_grad():
for images, labels in student_test_loader:
log_ps = student_model(images)
test_loss += criterion(log_ps, labels).item()
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
student_model.train()
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Train Loss: {:.3f}.. ".format(running_loss/len(student_train_loader)),
"Test Loss: {:.3f}.. ".format(test_loss/len(student_test_loader)),
"Accuracy: {:.3f}".format(accuracy/len(student_test_loader)))
running_loss = 0
Epoch: 1/10.. Train Loss: 0.321.. Test Loss: 3.638.. Accuracy: 0.217
Epoch: 1/10.. Train Loss: 0.254.. Test Loss: 5.541.. Accuracy: 0.217
Epoch: 1/10.. Train Loss: 0.244.. Test Loss: 5.642.. Accuracy: 0.217
Epoch: 2/10.. Train Loss: 0.223.. Test Loss: 5.961.. Accuracy: 0.217
Epoch: 2/10.. Train Loss: 0.205.. Test Loss: 6.295.. Accuracy: 0.254
Epoch: 2/10.. Train Loss: 0.186.. Test Loss: 6.514.. Accuracy: 0.303
...Now we will perform PATE Analysis on the student labels generated by the Aggregated Teacher
from syft.frameworks.torch.dp import pate
data_dep_eps, data_ind_eps = pate.perform_analysis(teacher_preds=preds, indices=student_labels, noise_eps=epsilon, delta=1e-5)
print("Data Independent Epsilon:", data_ind_eps)
print("Data Dependent Epsilon:", data_dep_eps)Which will give the output:
Data Independent Epsilon: 1451.5129254649705
Data Dependent Epsilon: 59.47392676433782Conclusion:
While performing different Differential privacy techniques it is important to note which technique to use in the given scenario. PATE is generally useful when a party wants to annotate a local data set using the private data sets of other actors, and the Epsilon-delta tool allows for very granular control of just how much the other actors must trust us to protect their privacy in this process.
Credits:
Nicolas Papernot - Private Machine Learning with PATE - Cybersecurity With The Best 2017
SCALABLE PRIVATE LEARNING WITH PATE paper
SEMI-SUPERVISED KNOWLEDGE TRANSFER FOR DEEP LEARNING FROM PRIVATE TRAINING DATA paper
A 5-Step Guide on incorporating Differential Privacy into your Deep Learning models
Nicolas Papernot and Ian goodfellow Clever-Hans blog
MAINTAINING PRIVACY IN MEDICAL DATA WITH DIFFERENTIAL PRIVACY
UNDERSTANDING DEEP LEARNING REQUIRES RETHINKING GENERALIZATION
Membership Inference Attacks Against Machine Learning Models
If you want to join our mission on making the world more privacy preserving:





